Punkta reizinājums

Matemātikā dot reizinājums ir operācija, kuras ievadā tiek ņemti divi vektori un kuras izejā tiek iegūts skalārs skaitlis. Atgūtais skaitlis ir atkarīgs no abu vektoru garuma un leņķa starp tiem. Nosaukums ir atvasināts no centrētā punkta "-", ko bieži izmanto, lai apzīmētu šo darbību; alternatīvais nosaukums skalārais reizinājums uzsver rezultāta skalāro (nevis vektoru) raksturu.

Punktu reizinājums (trīsdimensiju telpā) ir pretstats savstarpējam reizinājumam, kura rezultāts ir vektors.

Definīcija

Divu vektoru a = [a₁ , a₂ , ..., a_n ] un b = [b₁ , b₂ , ..., b_n ] dot reizinājums ir definēts kā:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}} $\mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

kur Σ apzīmē summācijas apzīmējumu (visu locekļu summa) un n ir vektoru telpas dimensija.

2. dimensijā vektoru [a,b] un [c,d] dot reizinājums ir ac + bd. Tāpat 3. dimensijā vektoru [a,b,c] un [d,e,f] punktu reizinājums ir ad + be + cf. Piemēram, divu trīsdimensiju vektoru [1, 3, -5] un [4, -2, -1] punktu reizinājums ir šāds.

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.} $[1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.$

Ģeometriskā interpretācija

Eiklīda ģeometrijā punktu reizinājums, garums un leņķis ir saistīti. Vektoram a punktu reizinājums a - a ir a garuma kvadrāts, vai

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}}} ${\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}$

kur ||a|| apzīmē a garumu (lielumu). Vispārīgāk, ja b ir cits vektors

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\|\cos \theta \,} $\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,$

kur ||a|| un ||b| apzīmē a un b garumu un θ ir leņķis starp tiem.

Šo formulu var pārkārtot, lai noteiktu leņķa lielumu starp diviem nenulles vektoriem:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}}\right\|\left\|{\mathbf {b}}}\right\|}}\right)} $\theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)$

Vektorus var arī vispirms pārvērst vienības vektoros, dalot ar to lielumu:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}}{\left\|{\mathbf {a}}}\right\|}}}} ${\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}$

tad leņķis θ ir dots ar

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}}cdot {\boldsymbol {\hat {b}}})} $\theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})$

Tā kā 90° kosinuss ir vienāds ar nulli, tad divu perpendikulāru vektoru dot reizinājums vienmēr ir vienāds ar nulli. Turklāt divus vektorus var uzskatīt par ortogonāliem tikai un vienīgi tad, ja to punktu reizinājums ir nulle un ja to garums nav nulle. Šī īpašība nodrošina vienkāršu metodi ortogonalitātes nosacījuma pārbaudei.

Dažreiz šīs īpašības izmanto arī punktu reizinājumam definēt, īpaši 2 un 3 dimensijās; šī definīcija ir līdzvērtīga iepriekš minētajai. Augstākām dimensijām šo formulu var izmantot, lai definētu leņķa jēdzienu.

Ģeometriskās īpašības balstās uz to, ka bāze ir ortonormāla, t. i., to veido perpendikulāri vektori ar vienības garumu.

Skalāra projekcija

Ja gan a, gan b garums ir viens (t. i., tie ir vienības vektori), tad to punktu reizinājums ir vienkārši leņķa starp abiem lielumiem kosinuss.

Ja tikai b ir vienības vektors, tad punktu reizinājums a - b dod |a| cos(θ), t. i., a projekcijas lielumu b virzienā ar mīnusa zīmi, ja virziens ir pretējs. To sauc par a skalāro projekciju uz b jeb a skalāro komponenti b virzienā (sk. attēlu). Šai punktu reizinājuma īpašībai ir vairāki noderīgi pielietojumi (piemēram, sk. nākamo nodaļu).

Ja ne a, ne b nav vienības vektors, tad, piemēram, a projekcijas lielums b virzienā būs a - (b / |b|), jo vienības vektors b virzienā ir b / |b|.

Rotācija

Ortonormālās bāzes rotāciju, ar kuras palīdzību tiek attēlots vektors a, iegūst, reizinot a ar rotācijas matricu R. Šī matricas reizināšana ir tikai punktu reizinājumu virknes kompakts attēlojums.

Piemēram, ļaujiet

B₁ = {x, y, z} un B₂ = {u, v, w} ir divas dažādas tās pašas telpas R³ ortonormālās bāzes, un B₂ iegūst, vienkārši pagriežot B₁ ,
a₁ = (a_x , a_y , a_z ) apzīmē vektoru a, izsakot B₁ ,
a₂ = (a_u , a_v , a_w ) apzīmē vienu un to pašu vektoru, izsakot pagrieztajā bāzē B₂ ,
u₁ , v₁ , w₁ ir pagriezti bāzes vektori u, v, w, kas izteikti ar B₁ .

Pēc tam rotāciju no B₁ uz B₂ veic šādi:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}}_{1}\{\{\mathbf {w}}_{1}\cdot {\mathbf {a}}}_{1}\end{bmatrix}}}={\begin{bmatrix}a_{u}\a_{v}\a_{w}\end{bmatrix}}}. } ${\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.$

Ievērojiet, ka rotācijas matrica R ir izveidota, izmantojot rotētos bāzes vektorus u₁ , v₁ , w₁ kā rindas, un šie vektori ir vienības vektori. Pēc definīcijas Ra₁ sastāv no punktu reizinājumu sekvences starp katru no trim R rindām un vektoru a₁ . Katrs no šiem punktu reizinājumiem nosaka a skalāro komponenti rotētā bāzes vektora virzienā (sk. iepriekšējo iedaļu).

Ja₁ ir rindas vektors, nevis kolonnas vektors, tad R ir jāietver rotētie bāzes vektori tā kolonnās un pēc tam jāreizina₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}}_{2}={\mathbf {a}}}_{1}{\mathbf {R}}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}}={{\begin{bmatrix}{\mathbf {u}}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. } ${\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.$

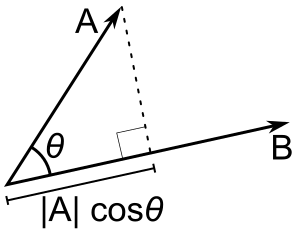
A - B = |A| |B| cos(θ). |A| cos(θ) ir A skalārā projekcija uz B.

Fizika

Fizikā lielums ir skalārs fizikālā nozīmē, t. i., fizikāls lielums, kas nav atkarīgs no koordinātu sistēmas un ko izsaka kā skaitliskās vērtības un fizikālās vienības reizinājumu, nevis tikai kā skaitli. Punktu reizinājums arī ir skalārs šajā nozīmē, ko nosaka ar formulu, neatkarīgi no koordinātu sistēmas. Piemērs:

Mehāniskais darbs ir spēka un pārvietojuma vektoru dotais reizinājums.
Magnētiskā plūsma ir magnētiskā lauka un laukuma vektoru punktveida reizinājums.
Tilpuma plūsmas ātrums ir šķidruma ātruma un laukuma vektoru punktveida reizinājums.

Īpašības

Ja a, b un c ir reāli vektori un r ir skalārs, ir spēkā šādas īpašības.

Punktveida reizinājums ir komutatīvs:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . } $\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .$

Punktveida reizinājums ir sadalošs pār vektoru saskaitīšanu:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . } $\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$

Punktveida reizinājums ir bilineārs:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). } $\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$

Ja reizina ar skalāru vērtību, dot reizinājums atbilst:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )} $(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )$

(pēdējās divas īpašības izriet no pirmajām divām).

Divi nenulles vektori a un b ir perpendikulāri tad un tikai tad, ja a - b = 0.

Atšķirībā no parasto skaitļu reizināšanas, kur, ja ab = ac, tad b vienmēr ir vienāds ar c, ja vien a nav nulle, punktu reizinājumam atcelšanas likums nav spēkā:

Ja a - b = a - c un a ≠ 0, tad pēc sadales likuma varam rakstīt: a - (b - c) = 0; iepriekš minētais rezultāts saka, ka tas nozīmē tikai to, ka a ir perpendikulārs (b - c), kas joprojām ļauj (b - c) ≠ 0, un tāpēc b ≠ c.

Ja bāze ir ortonormāla, punktu reizinājums ir nemainīgs, mainot bāzi izometriski: rotācijas, atstarojumi un kombinācijas, saglabājot nemainīgu sākumpunktu. Iepriekš minētā ģeometriskā interpretācija balstās uz šo īpašību. Citiem vārdiem sakot, ortonormālai telpai ar jebkuru dimensiju skaitu punktu reizinājums ir invariants koordinātu transformācijai, kuras pamatā ir ortogonāla matrica. Tas atbilst šādiem diviem nosacījumiem:

Jaunā bāze atkal ir ortonormāla (t.i., tā ir ortonormāla, izteikta vecajā bāzē).
Jaunajiem bāzes vektoriem ir tāds pats garums kā vecajiem (t. i., vienības garums vecās bāzes izteiksmē).

Ja a un b ir funkcijas, tad a - b atvasinājums ir a' - b + a - b'.

Trīskāršā produkta paplašināšana

Šī ir ļoti noderīga identitāte (pazīstama arī kā Lagranža formula), kas ietver dot- un šķērsproduktus. To izsaka šādi

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )} $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$

ko ir vieglāk atcerēties kā "BAC mīnus CAB", paturot prātā, kuri vektori ir punktēti kopā. Šo formulu parasti izmanto, lai vienkāršotu vektoru aprēķinus fizikā.

Ģeometriskās interpretācijas pierādījums

Aplūkojiet R elementu ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}}. _{1}+v_{2}\mathbf {\hat {e}}} _{2}+...+v_{n}\mathbf {\hat {e}}} _{n}.\,} $\mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,$

Atkārtoti piemērojot Pitagora teorēmu, tā garumam |v| tiek iegūts

| v | 2 = v 1 2 + v 2 2 + . . . . + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,} $|\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,$

Bet tas ir tas pats, kas

v ⋅ v = v 1 2 + v 2 2 + . . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,} $\mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,$

Tātad mēs secinām, ka, ņemot vektora v punktu reizinājumu ar sevi pašu, iegūstam vektora garumu kvadrātā.

Lemma 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,} $\mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,$

Tagad aplūkojiet divus vektorus a un b, kas stiepjas no sākumpunkta un ir atdalīti ar leņķi θ. Trešo vektoru c var definēt šādi

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\\\\mathbf {a} -\mathbf {b} .\,} $\mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,$

veido trijstūri ar malām a, b un c. Saskaņā ar kosinusa likumu iegūstam šādus lielumus

| c | 2 = | a | 2 + | b | 2 - 2 | a | | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $|\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Aizstājot punktu reizinājumus kvadrātveida garumiem saskaņā ar 1. Lemmu, mēs iegūstam.

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$ (1)

Bet, tā kā c ≡ a - b, mums arī ir

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} $\mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,$ ,

kas saskaņā ar sadales likumu paplašinās līdz

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,$ (2)

Apvienojot abus c - c vienādojumus, (1) un (2), iegūstam.

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

No abām pusēm atņemot a - a + b - b un dalot ar -2, iegūstam

a ⋅ b = | a | | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Q.E.D.

Apkopojums

Iekšējais reizinājums vispārina punktu reizinājumu abstraktām vektoru telpām un parasti tiek apzīmēts ar ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b}. \rangle } $\langle \mathbf {a} \,,\mathbf {b} \rangle$ . Ņemot vērā punkta reizinājuma ģeometrisko interpretāciju, vektora a normu ||a||| šādā iekšējā reizinājuma telpā definē šādi.

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={{\sqrt {\langle \\mathbf {a} \,,\mathbf {a} \rangle }}} $\|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}$

tā, ka tas vispārina garumu, un leņķi θ starp diviem vektoriem a un b ar

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} {{\\|\\mathbf {a} \|\,\|\\\mathbf {b} \|}}. } $\cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.$

Jo īpaši divus vektorus uzskata par ortogonāliem, ja to iekšējais reizinājums ir vienāds ar nulli.

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.} $\langle \mathbf {a} \,,\mathbf {b} \rangle =0.$

Vektoriem ar kompleksiem ierakstiem dotā punkta reizinājuma definīcija dotu pavisam citas ģeometriskās īpašības. Piemēram, vektora dot reizinājums ar sevi var būt patvaļīgs kompleksais skaitlis, un tas var būt nulle, ja vektors nav nulles vektors; tas savukārt radītu nopietnas sekas tādiem jēdzieniem kā garums un leņķis. Daudzas ģeometriskās īpašības var glābt, atsakoties no skalārā reizinājuma simetriskajām un bilineārajām īpašībām, alternatīvi definējot

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}} $\mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}$

kur b_i ir b _ikompleksais konjugāts. Tad jebkura vektora skalārais reizinājums ar sevi pašu ir nenoliedzošs reāls skaitlis, un tas ir nenulle, izņemot nulles vektoru. Tomēr šis skalārais reizinājums nav lineārs b (bet gan konjugēts lineārs), un skalārais reizinājums nav arī simetrisks, jo

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}} $\mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}$ .

Tomēr šāda veida skalārais reizinājums ir diezgan noderīgs, un tā rezultātā rodas Hermita formas un vispārējā iekšējā reizinājuma telpas jēdzieni.

Frobenija iekšējais reizinājums vispārina punktu reizinājumu matricām. To definē kā divu vienāda lieluma matricu atbilstošo komponenšu reizinājumu summu.

Vispārināšana uz tenzoriem

N kārtas tenzora un m kārtas tenzora dot reizinājums ir n+m-2 kārtas tenzors. Punktu reizinājumu iegūst, reizinot un saskaitot vienu indeksu abos tenzoros. Ja A {\displaystyle \mathbf {A} } $\mathbf {A}$ un B {\displaystyle \mathbf {B} } $\mathbf {B}$ ir divi tenzori ar elementu attēlojumu A i j ... k ℓ ... {\displaystyle A_{{ij\dots }^{k\ell \dots }} $A_{ij\dots }^{k\ell \dots }$ un B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}} $B_{mn\dots }^{p{\dots }i}$ punktu reizinājuma A ⋅ B {\displaystyle \mathbf {A} elementi. \cdot \mathbf {B} } $\mathbf {A} \cdot \mathbf {B}$ ir dots ar

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}}} $A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}$

Šī definīcija, protams, reducējas uz standarta vektoru punktu reizinājumu, ja to piemēro vektoriem, un matricu reizinājumu, ja to piemēro matricām.

Dažkārt tiek izmantots dubultais punktveida reizinājums, lai attēlotu divu indeksu reizināšanu un saskaitīšanu. Divkāršais punktu reizinājums starp diviem 2. kārtas tenzoriem ir skalārs.

Saistītās lapas

Kohī-Švarca nevienlīdzība
Šķērsprodukts
Matricu reizināšana
Fizika

Jautājumi un atbildes

J: Kas matemātikā ir punktu reizinājums?

A: Punktu reizinājums ir operācija, kurā kā ieejas dati tiek ņemti divi vektori un kā izejas dati tiek atgriezts skalārs skaitlis.

J: No kā ir atkarīgs dot reizinājums?

O: Punktu reizinājums ir atkarīgs no abu vektoru garuma un leņķa starp tiem.

J: Kāpēc dot reizinājuma nosaukums ir atvasināts no centrētā punkta "-"?

A: Nosaukums ir atvasināts no centrētā punkta "-", ko bieži izmanto, lai apzīmētu šo darbību.

J: Kāds ir alternatīvais dot reizinājuma nosaukums?

A: Alternatīvais nosaukums ir skalārais reizinājums, kas uzsver rezultāta skalāro (nevis vektoru) raksturu.

J: Kāda ir atšķirība starp punktu reizinājumu un šķērsvienādojumu trīsdimensiju telpā?

A: Punktu reizinājums kā rezultātu dod skalāru skaitli, bet krusteniskais reizinājums kā rezultātu dod vektoru.

J: Kādam nolūkam matemātikā izmanto punktu reizinājumu?

A: Punktu reizinājumu var izmantot, lai noteiktu, vai divi vektori ir perpendikulāri (veido 90 grādu leņķi), un lai projicētu vienu vektoru uz otru.

J: Vai punktu reizinājumu var izmantot augstākas dimensijas telpās?

A: Jā, punktu reizinājumu var attiecināt arī uz augstākas dimensijas telpām, vispārinot definīciju.