Harmoniskā virkne (matemātika)

Vēsture

To, ka harmoniskā virkne atšķiras, pirmo reizi 14. gadsimtā pierādīja Nikols Oresme, taču tas tika aizmirsts. Pierādījumus 17. gadsimtā sniedza Pjetro Mengoli, Johans Bernuili un Jakobs Bernuili.

Arhitekti ir izmantojuši harmoniskās secības. Baroka laikmetā arhitekti tās izmantoja proporcijās starp stāvu plāniem, fasādēm, kā arī baznīcu un piļu arhitektūras detaļu attiecībās.

Diverģence

Ir vairāki labi zināmi harmoniskās rindas diverģences pierādījumi. Daži no tiem ir sniegti turpmāk.

Salīdzināšanas tests

Viens no veidiem, kā pierādīt diverģenci, ir salīdzināt harmonisko rindu ar citu diverģējošu rindu, kurā katrs saucējs ir aizstāts ar nākamo lielāko divu lielumu:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}}+{\frac {1}{6}}+{\frac {1}{7}}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{{\frac {1}{2}}+{\frac {1}{krāsa {sarkana}{\mathbf {4} }}}+{{\frac {1}{4}}+{{\frac {1}{\color {red}{\mathbf {8}} }}}+{{\frac {1}{{krāsa {red}{\mathbf {8}} }}}+{{\frac {1}{\krāsa {red}{\mathbf {8}} }}}+{{\frac {1}{8}}}+{{\frac {1}{krāsa {arkana}{\mathbf {16}} }}}+\cdots \end{aligned}}}

Katrs harmoniskās rindas loceklis ir lielāks vai vienāds ar atbilstošo otrās rindas locekli, tāpēc harmoniskās rindas summai jābūt lielākai vai vienādai ar otrās rindas summu. Tomēr otrās rindas summa ir bezgalīga:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}}right)+\left({\frac {1}{4}}}!+\!{\frac {1}{4}}}\right)+\left({\frac {1}{8}}}\!+\!{\!{\frac {1}{8}}}\!+\!{\frac {1}{8}}}\!+\!{\frac {1}{8}}}\right)+\left({\frac {1}{16}}}\!+\!\cdots \!+\!{\frac {1}{16}}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}}

No tā izriet (pēc salīdzināšanas testa), ka arī harmonisko rindu summai jābūt bezgalīgai. Precīzāk, iepriekš minētais salīdzinājums pierāda, ka

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}}ģeq 1+{\frac {k}{2}}}}.

katram pozitīvam veselam skaitlim k.

Šis pierādījums, ko Nikolā Oresme ierosināja ap 1350. gadu, tiek uzskatīts par viduslaiku matemātikas virsotni. Tas joprojām ir standarta pierādījums, ko māca matemātikas stundās.

Integrāls tests

Ir iespējams pierādīt, ka harmoniskā virkne atšķiras, salīdzinot tās summu ar nepiemērotu integrāli. Aplūkojiet taisnstūru izkārtojumu, kas parādīts attēlā pa labi. Katrs taisnstūris ir 1 vienības plats un 1/n vienības augsts, tāpēc bezgalīgi daudzu taisnstūru kopējais laukums ir harmoniskās virknes summa:

taisnstūru laukums = 1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{a laukums}}\\\{\text{taisnstūri}}}\end{array}}}=1+{{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }

Kopējais laukums zem līknes y = 1/x no 1 līdz bezgalībai ir dots ar diverģējošu nepareizu integrālu:

laukums zem līknes = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{platība zem}}}\\{\text{krāsa}}}\end{array}}}=\int _{1}^{\infty }{\frac {1}{x}}},dx=\infty . }

Tā kā šī platība pilnībā ietilpst taisnstūros, tad arī taisnstūru kopējai platībai jābūt bezgalīgai. Tas pierāda, ka

∑ n = 1 k 1 n > ∫ 1 k + 1 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}},dx=\ln(k+1). }

Šā argumenta vispārinājums ir pazīstams kā integrālais tests.

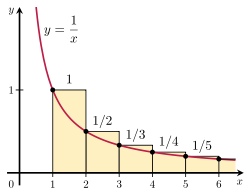
Integrālā testa ilustrācija.

Atšķirības ātrums

Harmoniskā virkne atšķiras ļoti lēni. Piemēram, pirmo 1043 locekļu summa ir mazāka par 100. Tas ir tāpēc, ka sērijas daļējām summām ir logaritmiska izaugsme. Konkrēti,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1}

kur γ ir Ēlera-Mašeroni konstante un εk ~ 1/2k, kas tuvojas 0, kad k tuvojas bezgalībai. Leonhards Eulers pierādīja gan to, gan arī to, ka arī summa, kas ietver tikai pirmatņu savstarpējos skaitļus, atšķiras, tas ir:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}}{{\frac {1}{p}}={\frac {1}{2}}}+{\frac {1}{3}}+{\frac {1}{5}}}+{\frac {1}{7}}+{\frac {1}{11}}}+{\frac {1}{13}}}+{\frac {1}{17}}}+\cdots =\infty . }

Daļējas summas

Pirmie trīsdesmit harmoniskie skaitļi
n	Harmonisko rindu daļējā summa, Hn
	izteikts kā daļa		decimālskaitļi	relatīvais lielums
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Galīgās harmonisko rindu noviržu galīgās daļējās summas,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}},}

sauc par harmoniskajiem skaitļiem.

Starpība starp Hn un ln n konverģē pie Ēlera-Mašeroni konstantes. Starpība starp jebkuriem diviem harmoniskajiem skaitļiem nekad nav vesels skaitlis. Neviens harmoniskais skaitlis nav vesels skaitlis, izņemot _H1 = 1.

Saistītās sērijas

Mainīgas harmoniskās sērijas

Sērija

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{{\infty }{\frac {(-1)^{n+1}}}{n}}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}}-\cdots }

ir pazīstama kā mainīgā harmoniskā virkne. Šī rinda konverģē pēc mainīgās rindas testa. Jo īpaši summa ir vienāda ar 2 dabisko logaritmu:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}}+{\frac {1}{3}}-{\frac {1}{4}}}+{\frac {1}{5}}-\cdots =\ln 2.}

Mainīgā harmoniskā rinda, lai gan nosacīti konverģējoša, nav absolūti konverģējoša: ja rindas locekļus sistemātiski pārkārto, kopumā summa kļūst atšķirīga un, atkarībā no pārkārtojuma, iespējams, pat bezgalīga.

Mainīgās harmoniskās rindas formula ir Merkatora rindas - dabiskā logaritma Teilora rindas - īpašs gadījums.

Saistītu rindu var atvasināt no Teilora rindas arktangentam:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}}{2n+1}}}=1-{\frac {1}{3}}+{\frac {1}{5}}}-{\frac {1}{7}}}+\cdots ={\frac {\pi }{4}}. }

To sauc par Leibnica virkni.

Vispārējās harmoniskās sērijas

Vispārējā harmoniskā rinda ir šāda

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},}

kur a ≠ 0 un b ir reālie skaitļi, un b/a nav nulle vai negatīvs vesels skaitlis.

Veicot robežu salīdzināšanas testu ar harmonisko rindu, visas vispārējās harmoniskās rindas arī atšķiras.

p sērija

Harmonisko rindu vispārinājums ir p rinda (vai hiperharmoniskā rinda), ko definē šādi.

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}}

jebkuram reālajam skaitlim p. Ja p = 1, p rinda ir harmoniskā rinda, kas atšķiras. Integrālais tests vai Košija kondensācijas tests parāda, ka p-rinda konverģē visiem p > 1 (šādā gadījumā to sauc par pārharmonisko rindu) un diverģē visiem p ≤ 1. Ja p > 1, tad p rindu summa ir ζ(p), t. i., Rīmana zetas funkcija, kas novērtēta pie p.

Uzdevumu atrast summu p = 2 sauc par Bāzeles uzdevumu; Leonhards Eulers parādīja, ka tā ir π2/6. Summas vērtību p = 3 sauc par Aperī konstanti, jo Rodžērs Aperī pierādīja, ka tā ir iracionāls skaitlis.

ln sērija

Ar p-rindu ir saistīta ln-rinda, ko definē šādi.

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}}

To var pierādīt ar integrālo testu, ka tas atšķiras, ja p ≤ 1, bet konverģē visiem p > 1.

φ sērija

Jebkurai izliektai reālas vērtības funkcijai φ, kas ir tāda, ka

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{{\frac {\varphi \left({\frac {u}{2}}}\right)}{\varphi (u)}}}<{\frac {1}{2}},}}

sērija

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}}\right)}

ir konverģents. ^[]

Nejaušas harmoniskās sērijas

Nejaušās harmoniskās rindas

∑ n = 1 ∞ s n n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}}{n}},}

kur _sn ir neatkarīgi, identiski sadalīti nejaušie lielumi, kas ar vienādu varbūtību 1/2 iegūst vērtības +1 un -1, ir labi zināms varbūtību teorijas piemērs nejaušo lielumu virknei, kas konverģē ar varbūtību 1. Šīs konverģences fakts ir vienkāršs Kolmogorova trīs rindu teorēmas vai cieši saistītās Kolmogorova maksimālās nevienādības rezultāts. Bairons Šmulands (Byron Schmuland) no Albertas Universitātes turpināja pētīt nejaušās harmoniskās rindas īpašības un parādīja, ka konverģējošā rinda ir nejaušs lielums ar dažām interesantām īpašībām. Jo īpaši šī nejaušā mainīgā varbūtības blīvuma funkcija, kas novērtēta pie +2 vai pie -2, iegūst vērtību 0,124999999999999999999999999999999999999999764..., kas atšķiras no 1/8 ar mazāk nekā 10-42. Šmulanda rakstā paskaidrots, kāpēc šī varbūtība ir tik tuvu 1/8, bet ne tieši 1/8. Precīzu šīs varbūtības vērtību nosaka ar bezgalīgo kosinizācijas reizinājuma integrāli _{C2, kas} dalīts ar π.

Izsīkusi harmonisko virkņu virkne

Var pierādīt, ka noplicinātā harmoniskā virkne, kurā visi locekļi, kuru saucējā jebkurā vietā parādās cipars 9, ir konverģējoši un tās vērtība ir mazāka par 80. Patiesībā, ja tiek izņemti visi locekļi, kas satur kādu konkrētu ciparu virkni (jebkurā bāzē), rinda konverģē.

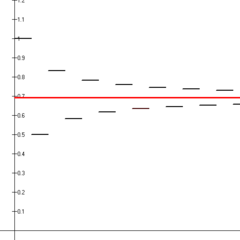
Pirmie četrpadsmit mainīgo harmonisko rindu pirmās četrpadsmit daļējās summas (melni līniju posmi), kas konverģē pie 2 dabiskā logaritma (sarkanā līnija).

Pieteikumi

Harmoniskā virkne var būt pretrunā ar intuīciju. Tas ir tāpēc, ka tā ir diverģējošā rinda, lai gan tās locekļi kļūst mazāki un tuvojas nullei. Harmoniskās rindas diverģence ir dažu paradoksu cēlonis.

• "Tārps uz gumijas". Pieņemsim, ka tārps rāpo pa bezgalīgi elastīgu viena metra garu gumijas lenti tajā pašā laikā, kad gumijas lente ir vienmērīgi izstiepta. Ja tārps pārvietojas 1 centimetru minūtē un gumijas lenta stiepjas 1 metru minūtē, vai tārps kādreiz sasniegs gumijas lentas galu? Atbilde ir "jā", jo pēc n minūtēm sliekas veiktā attāluma attiecība pret gumijas lentes kopējo garumu ir šāda.

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}}. }

Tā kā virkne kļūst patvaļīgi liela, jo n kļūst lielāks, šai attiecībai galu galā ir jāpārsniedz 1, kas nozīmē, ka tārps sasniedz gumijas galu. Tomēr n vērtībai, pie kuras tas notiek, jābūt ārkārtīgi lielai: aptuveni e100, skaitlim, kas pārsniedz 1043 minūtes (1037 gadus). Lai gan harmoniskā rinda atšķiras, tas notiek ļoti lēni.

• Džipa uzdevums ir noskaidrot, cik daudz kopējās degvielas ir nepieciešams, lai automašīna ar ierobežotu degvielas ietilpību varētu šķērsot tuksnesi, atstājot degvielas pilienus pa ceļam. Attālums, ko automašīna var nobraukt ar doto degvielas daudzumu, ir saistīts ar harmonisko rindu daļējām summām, kas aug logaritmiski. Tādējādi nepieciešamā degviela pieaug eksponenciāli, palielinoties vēlamajam attālumam.

• Bloku sakraušanas problēma: ja ir vienādu domino kauliņu kolekcija, ir iespējams tos sakraut galda malā tā, lai tie karājas pāri galda malai un nenokrīt. Pretēji intuīcijai rezultāts ir tāds, ka tās var sakraut tā, lai pārkare būtu tik liela, cik vien vēlaties. Tas ir, ar nosacījumu, ka ir pietiekami daudz domino kauliņu.

• Peldētājs, kurš ar katru pieskārienu baseina sienai peld ātrāk. Peldētājs sāk pārvarēt 10 metru baseinu ar ātrumu 2 m/s, un ar katru pārvarēšanu ātrums palielinās vēl par 2 m/s. Teorētiski peldētāja ātrums ir neierobežots, bet baseina šķērsošanas reižu skaits, kas nepieciešams, lai sasniegtu šo ātrumu, kļūst ļoti liels; piemēram, lai sasniegtu gaismas ātrumu (neņemot vērā speciālo relativitāti), peldētājam baseins jāpārlec 150 miljonus reižu. Pretēji šim lielajam skaitlim, laiks, kas nepieciešams, lai sasniegtu noteiktu ātrumu, ir atkarīgs no sērijas saskaitīšanas pie jebkura konkrētā baseina šķērsošanas skaita:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}}. }

Aprēķinot summu, izrādās, ka laiks, kas nepieciešams, lai sasniegtu gaismas ātrumu, ir tikai 97 sekundes.

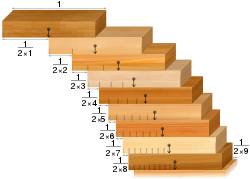
Bloku kārtošanas problēma: bloki, kas sakārtoti saskaņā ar harmonisko virkni, savieno jebkura platuma šķēlumus.

Saistītās lapas

• Harmoniskā progresija
• Recircinālu summu saraksts